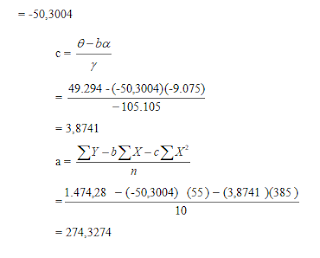Peramalan Indeks Harga Konsumen Kota Bandar Lampung untuk Tahun 2017 dan 2018
4.1.1. PeramalanIndeks Harga Konsumen Kota Bandar
Lampung
Data besarnya Indeks Harga Konsumen Kota Bandar Lampung dari tahun
2003-2012 dapat dilihat pada Tabel 4.1.
Tabel 4.1.Indeks
Harga Konsumen Kota Bandar Lampung
Tahun
|
Indeks Harga
Konsumen
|
2003
|
294,11
|
2004
|
112,68
|
2005
|
125,69
|
2006
|
145,25
|
2007
|
152,69
|
2008
|
112,14
|
2009
|
120,32
|
2010
|
128,49
|
2011
|
138,63
|
2012
|
144,28
|
Langkah-langkah
peramalan yang dilakukan terdiri atas :
1. Mendefinisikan
tujuan peramalan
Tujuan
peramalan adalah untuk meramalkan Indeks Harga Konsumen Kota Bandar Lampung pada
tahun 2017 ( pada periode (x) = 15) dan
2018 ( pada periode (x) = 16) .
2. Pembuatan Scatter diagram
Daridata Indeks Harga Konsumen pada Tabel 4.1 maka dibuat
scatter diagram untuk melihat pola data.
Gambar 4.1. Scatter Diagram Indeks Harga Konsumen Kota
Bandar Lampung
3. Pemilihan Metode Peramalan
Metode peramalan yang digunakan adalah :
a. Metode linear
b. Metode kuadratis
4. Menghitung parameter peramalan
Untuk memudahkan perhitungan, maka dimisalkan X
sebagai variabel tahun dan Y sebagai variabel basarnyaIndeks Harga Konsumen.
a. Metode linier
Fungsi
peramalan : Y = a + bx
Tabel
4.2. Perhitungan Parameter Peramalan Indeks Harga Konsumen MetodeLinier
x
|
Y
|
x.Y
|
x2
|
1
|
294,11
|
294,11
|
1
|
2
|
112,68
|
225,36
|
4
|
3
|
125,69
|
377,07
|
9
|
4
|
145,25
|
581,00
|
16
|
5
|
152,69
|
763,45
|
25
|
6
|
112,14
|
672,84
|
36
|
7
|
120,32
|
842,24
|
49
|
8
|
128,49
|
1.027,92
|
64
|
9
|
138,63
|
1.247,67
|
81
|
10
|
144,28
|
1.442,80
|
100
|
55
|
1.474,28
|
7.474,46
|
385
|
Fungsi peramalan : Y’ = 189,6999-76858x
b. Metode kuadratis
Fungsi
peramalan: Y’
= a + bx + cx2
Tabel 4.3. Perhitungan Parameter Peramalan Indeks Harga
Konsumen Metode Kuadratis
x
|
Y
|
x2
|
x3
|
x4
|
x.Y
|
x2.Y
|
1
|
294,11
|
1
|
1
|
1
|
294,11
|
294,11
|
2
|
112,68
|
4
|
8
|
16
|
225,36
|
450,72
|
3
|
125,69
|
9
|
27
|
81
|
377,07
|
1131,21
|
4
|
145,25
|
16
|
64
|
256
|
581
|
2324
|
5
|
152,69
|
25
|
125
|
625
|
763,45
|
3817,25
|
6
|
112,14
|
36
|
216
|
1296
|
672,84
|
4037,04
|
7
|
120,32
|
49
|
343
|
2401
|
842,24
|
5896
|
8
|
128,49
|
64
|
512
|
4096
|
1027,92
|
8223,36
|
9
|
138,63
|
81
|
729
|
6561
|
1247,67
|
11229,03
|
10
|
144,28
|
100
|
1000
|
10000
|
1442,8
|
14428
|
55
|
1474,28
|
385
|
3025
|
25333
|
7474,46
|
51830
|
Fungsi
peramalannya adalah:
Y’= 274,3274– 50,3004x+3,8741x2
5. Menghitung
setiap kesalahan setiap metode
Perhitungan kesalahan menggunakan metode SEE (StandardErrorofEstimate) dan PE (Percentage Error)dengan menggunakan rumus sebagai berikut:
Keterangan :
y = data aktual
y’ = data peramalan
n = banyak data
f = derajat kebebasan
a. Metode Linier (f = 2)
Adapun perhitungan
SEE dan PE untuk metode linier adalah:
Tabel 4.4. Perhitungan SEEdan PE Indeks Harga Konsumen untuk
Metode Linier
X
|
Y
|
Y'
|
Y-Y'
|
(Y-Y')2
|
PE
|
1
|
294,11
|
182,0141
|
112,0959
|
12565.4908
|
38,1136
|
2
|
112,68
|
174,3283
|
-61,6483
|
3800.5129
|
-54,7110
|
3
|
125,69
|
166,6425
|
-40,9525
|
1677.1073
|
-32,5821
|
4
|
145,25
|
158,9567
|
-13,7067
|
187.8736
|
-9,4366
|
5
|
152,69
|
151,2709
|
1,4191
|
2.0138
|
0,9294
|
6
|
112,14
|
143,5851
|
-31,4451
|
988.7943
|
-28,0409
|
7
|
120,32
|
135,8993
|
-15,5793
|
242.7146
|
-12,9482
|
8
|
128,49
|
128,2135
|
0,2765
|
0.0765
|
0,2152
|
9
|
138,63
|
120,5277
|
18,1023
|
327.6933
|
13,0580
|
10
|
144,28
|
112,8419
|
31,4381
|
988.3541
|
21,7896
|
55
|
1474,2800
|
1474,2800
|
0,0000
|
20780,6312
|
-63,6130
|
b. Metode Kuadratis ( f = 3 )
Adapun perhitungan SEE dan PEuntuk metode kuadratis, yaitu :
Tabel 4.5. Perhitungan SEEdan PE Indeks Harga Konsumen untuk
Metode Kuadratis
x
|
Y
|
Y'
|
Y-Y'
|
(Y-Y')2
|
PE
|
1
|
294,1100
|
228,5011
|
65,6089
|
4304,5278
|
22,3076
|
2
|
112,6800
|
189,8230
|
-77,1430
|
5951,0424
|
-68,4620
|
3
|
125,6900
|
158,8931
|
-33,2031
|
1102,4458
|
-26,4167
|
4
|
145,2500
|
135,7114
|
9,5386
|
90,9849
|
6,5670
|
5
|
152,6900
|
120,2779
|
32,4121
|
1050,5442
|
21,2274
|
6
|
112,1400
|
112,5926
|
-0,4526
|
0,2048
|
-0,4036
|
7
|
120,3200
|
112,6555
|
7,6645
|
58,7446
|
6,3701
|
8
|
128,4900
|
120,4666
|
8,0234
|
64,3749
|
6,2444
|
9
|
138,6300
|
136,0259
|
2,6041
|
6,7813
|
1,8785
|
10
|
144,2800
|
159,3334
|
-15,0534
|
226,6049
|
-10,4335
|
55
|
1474,2800
|
1474,2805
|
-0,0005
|
12856,2556
|
-41,1208
|
Gambar 4.2. Grafik Uji Hipotesis
Indeks Harga Konsumen dengan
Distribusi F
Oleh karena Fhitung(0,6464)<Ftabel (3,73), maka Ho
diterima. Jadi hasil pengujian menyatakan bahwa metode kuadratis
lebih baik daripada metode linier.
Adapun fungsi kuadratis tersebut adalah
sebagai berikut:
Y’= 274,3274–
50,3004 x+3,8741x2
7. Verifikasi peramalan
Tujuan proses verifikasi
dilakukan adalah untuk mengetahui apakah fungsi yang telah ditentukan dapat
mewakili data yang akan diramalkan.
Tabel 4.6. Perhitungan Hasil Verifikasi Peramalan Indeks
Harga Konsumen
x
|
Y
|
Y'
|
Y-Y'
|
MR
|
1
|
294,11
|
228,5011
|
65,6089
|
-
|
2
|
112,68
|
189,8230
|
-77,1430
|
142,7519
|
3
|
125,69
|
158,8931
|
-33,2031
|
43,9399
|
4
|
145,25
|
135,7114
|
9,5386
|
42,7417
|
5
|
152,69
|
120,2779
|
32,4121
|
22,8735
|
6
|
112,14
|
112,5926
|
-0,4526
|
32,8647
|
7
|
120,32
|
112,6555
|
7,6645
|
8,1171
|
8
|
128,49
|
120,4666
|
8,0234
|
0,3589
|
9
|
138,63
|
136,0259
|
2,6041
|
5,4193
|
10
|
144,28
|
159,3334
|
-15,0534
|
17,6575
|
55
|
1474,28
|
1474,2805
|
-0,0005
|
316,7245
|
Gambar
4.3.
Moving Range Chart Indeks
Harga Konsumen di Kota Bandar Lampung
Terlihat keseluruhan titik hasil peramalan telah berada dalam batas sehingga peramalan dengan metode
kuadratis cukup memenuhi persyaratan dengan fungsi
peramalan :
Y’= 274,3274–
50,3004 x+3,8741x2
Sehingga ramalan Indeks
Harga Konsumen di Kota Bandar
Lampung pada tahun 2017 ( pada periode (x) = 15) adalah sebagai
berikut :
Y’
= 274,3274 – 50,3004 (15) + 3,8741 (15)2
Y’ =
392,0939 »
392,09
Sehingga ramalan Indeks Harga Konsumen
di Kota Bandar Lampung pada tahun
2018 ( pada periode (x) = 16) adalah
sebagai berikut :
Y’
= 274,3274 – 50,3004 (16) + 3,8741 (16)2
Y’ =
461,8906 » 461,89